数据结构（data structure）将数据通过某种形式组织起来，从而使我们基于其封装的接口进行操作；比如，通过线形结构（stack，queue）能够约束我们访问数据的顺序，通常可用在concurrency program的同步中；而树形结构给与我们最大的能力就是以非 O(N) 的复杂度检索数据，有各种各样的Tree，笔者将其分为两种：

基于比较器判断来定位，用户有自定义比较器的灵活性，也带来了比较器的开销。
1. 比较Key，就是Tree类型的，考虑的维度有：几个叉、是否平衡等
2. 比较Hash，就是hash表，考虑如何处理冲突。
基于key本身信息（byte or bit）直接定位，一般就是通过前缀，这样实际就约束了用户只能使用Bytewise比较器，但是消除了比较器的开销；但是存在一个共同的问题——如何解决前缀相同的key的匹配。
1. Prefix tree（trie）
2. RadixTree、Patricia Tree

本文介绍的CritBit Tree属于类别2b，巧妙地对Prefix Tree进行抽象，大大节约了存储空间占用。在介绍CritBitTree之前，先对类别2共同的问题今天简单探讨，常见的方式就是通过再编码转换，这是数据库中常用的技术，可以参考MyRocks中的Record Format，其采用了prefix length的方式；但是prefix需要添加一个用户不需要的bytes。这里介绍一个巧妙的编码方式KART；因为当prefix相同时，我们的难点在于不知道byte Sequence在何处结束；那么在byte sequence的每个byte前加一个1 bit，在末尾补一个0 bit；这种方式不需要真的存下来，只需要在计算出每个位置的bit值即可区分出前缀。

unsigned int bit(size_t pos, unsigned char const* k, size_t klen) {
  if (pos/(CHAR_BIT+1)>=klen) return 0;
  if (pos%(CHAR_BIT+1)==0) return 1;
  return (((unsigned int)k[pos/(CHAR_BIT+1)])>>(CHAR_BIT-pos%(CHAR_BIT+1)))&(unsigned int)1;
}

解决的编码问题后，那么，什么是CritBit？

Critbit Tree

在Prefix Tree中，字符串K1本身就代表了Tree的遍历路径；如果路径不匹配，那么K1就不在Tree中；而如果Prefix Tree存在很多共同前缀，可以考虑进行路径压缩来节约空间，从而得到Radix Tree；对于当前数据集，这些被压缩的位置上的字符不能提供检索信息，那么对于定位来说，其实可以不存，反之只存产生分歧的位置。而如果只存储分歧点的话，为了进一步压缩，将Byte展开成Bit，产生分歧的位置（下标）就是 Crit(ical)Bit。

在CritBitTree中，每个Node中存储一个CritBit和两个child，分别代表CritBit=0和1；整个树需要保证ChildNode.critbit > parentNode.critbit，这样保证了CritBitTree的字典序，如下：

struct Node {
	void* child[2];
	uint32_t byte;
	uint8_t otherbits;
} Node;

这里通过byte + otherbits表示CritBit的位置，otherbits是一个CritBit的mask（CritBit处为0，其他位为1），这样可以通过otherbits方便的取得CritBit信息。

举个简单的例子，如下图，当定位1000是否在Tree中时，先查看下标为0的bit，发现是1，决定走child[1];然后查看下标为2的bit，发现是0，决定走child[0]；和Prefix Tree类似，定位到最终的位置后，还是需要比较Suffix，判断是否Match。

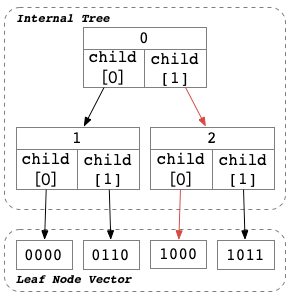
值得注意的是CritBit Tree只包含了CritBit，并没有保存完整的Prefix；只要我们保证CritBit按顺序访问，那么一个数据集有且仅有一个CritBit Tree表示；当新Key有个一个完全不同的CritBit，那么基于已有的CritBit信息，得到的最终LeafNode有可能是Unmatched。

对于insert场景，如果首次定位Unmatch，此时记下了访问过的NodePath，则需再根据找到的unmatch_key与target得到NewCritBit，当target[NewCritbit]=1，则将NodePath中CritBit > NewCritbit的子树挂在NewNode.child[0]下，反之同理，这样就完成了Insert操作；同理lower_bound的查询同样有可能需要两次定位，只是第二次定位需要一直遍历到其子树的叶子节点才是lower_bound，即，当target[NewCritBit]=0时，就是新右子树的最左节点；当target[NewCritBit]=1时，就是新左子树的最右节点+1。

另外，对于Tree类型的数据结构，都有一个cache miss的问题；特别是对于不平衡的Prefix Tree类型；可将Hash与CritBitTree结合，将每个CritBitTree容量减小，如果能全部塞到Cacheline里就更好了；TerarkDB中将succinct与CritBitTree结合，进一步压缩了CritBitTree的空间，本文对其进行简单介绍。

TerarkDB Impl

TerarkDB中有大量Succinct算法，这里对Succinct进行简单概括，知道这是个什么，能提供什么能力即可。

Succinct Algo

In computer science, a succinct data structure is a data structure which uses an amount of space that is “close” to the information-theoretic lower bound, but (unlike other compressed representations) still allows for efficient query operations.

我的理解就是将传统数据结构通过某种编码方式转换为bitvector，然后基于bitvector的基本操作：RSA（rank/select/access）进行查询的算法；这样能极大节约内存，并且还能保证较好的响应速度；那么，对于一个Bitvector，有以下三个基本操作：

rank(position)：position之前（不包括position）有多少个bitval；如果bitval=1代表一个有效元素，那么我们通过rank<1>(position)，可知position前有多少个有效元素。
select(rankval):rank(?position) == rankval的position中**最大**的；这样我们可以知道第rankval个有效元素，位于bitvector的什么位置。
access(position)：简单的数组下标访问。

rank/select的具体实现最简单的是遍历bitvector，但是这样效率必然低下，通常采用分段预计算的方式进行优化，这个就不展开了；由此我们知道如何在bitvector上进行检索；那么，我们可以将一些数据结构编码成bitvector，这里介绍一种树的编码方式——LOUDS。

LOUDS（Level-Ordered Unary Degree Sequence）逐层遍历多叉树，如果节点有D个子节点，那么bitvector追加 D个1 + 一个0；如下图：

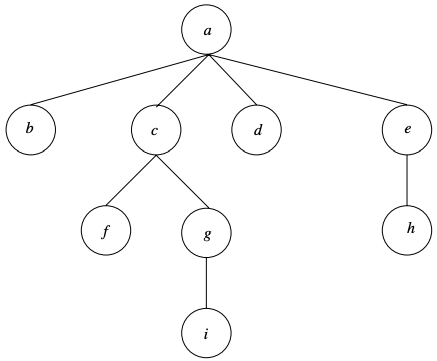
这里假设有一个虚拟的super root，那么对于super root节点，其有一个子节点（即,a），那么追加”10”；对于a，有四个子节点，那么追加”11110”；对于b，没有子节点，那么追加”0”；以此类推，最终得到如下bitvector。

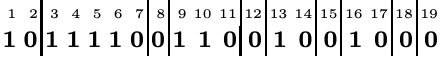
通过rank/select的组合调用即可完成树的检索，比如Node_c的编号是4（=实际下标+1），可通过select<0>(rank<1>(4))+1得到其firstchild，尝试来理解一下：首先通过rank<1>(4)得到自己是第3个节点；由于每个节点编码时都有且只有一个0，然后通过select<0>(3)定位到第3个0的位置，每个0代表一个子节点组，其中包括第一个super_root的子节点组；那么第三个0就是b节点的子节点组，因此，其之后就是Node_c的子节点组，那么第一个就是firstchild。

CBT in TerarkDB

TerarkDB中分别将Internal Tree结构和叶子节点进行编码，得到两个BitArray：

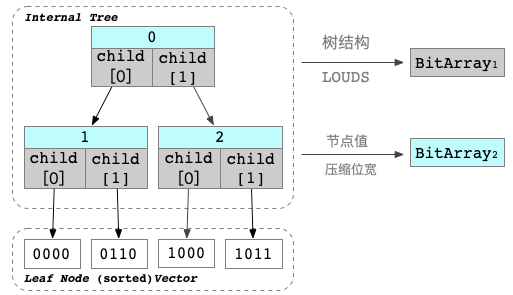
BitArray_1 ：采取类似LOUDS的层序遍历将二叉树转换为bitvector；LOUDS每个节点有且只有一个0，terark对于每个节点有且只有两个bit，有效子节点为1，无效节点为0；比如上图的bitarray就是”11,00,00”。
BitArray_2：对于每个节点内的CritBit，先取了Delta，值域理论上变小，即更少的位宽即可表示一个整数，因此可以用压缩位宽的UintVec进行存储；

最终通过树的检索得到叶子节点在全局的序号，就是该具体数据的SortedVector的下标。

Build

因为CritBitTree在TerarkDB中，主要用在SST中，而且我们知道SST的构建是MergeSort的结果，其输入是有序的（假设升序），那么在构建的过程中，预期下层的CritBit比上层大（CurrentKey.CritBit > CurrentNode.CritBit），那么，当CritBit相同时，比较下一个CritBit始终选择右子树；当CurrentKey.CritBit < CurrentNode.CritBit，创建一个NewNode替换CurrentNode，NewNode.CritBit = CurrentKey.CritBit；NewNode.leftChild = CurrentNode。

Search

CritBitTree只是一个索引，LeafValue存储在一个value_vector的中，索引只需要找到Key在vector中的下标即可。通过上节的编码方式可知，其实无效节点就对应一个leafnode ，这样统计每层左侧有几个leafnode，就得到Key在整个value_vector中的序号（要落到最深底层，因为对于右子树浅的情况，会提前退出）；对于Get来说，找到key在原始有序input中的序号，进一步反问比较是否match，这里有个可选的优化，可以存N个bit的hash进行过滤。对于Seek（lower_bound）来说，TerarkDB在第一次Get定位时，保存了best_match_key；如果unmatch，则比较best_match_key与target_key，可直接得知common_prefix_bit，从而继续向下定位。

以上笔者用较短的篇幅简单概括了CritBitTree的原理，如果感兴趣可以参考https://github.com/agl/critbit和https://github.com/bytedance/terarkdb的代码进行更细节的了解。

Yangming's Blog

CritBitTree