Paper:Main-Memory Hash Joins on Multi-Core CPUs: Tuning to the Underlying Hardware
数据库的计算层常常通过并行的方式降低查询延迟,并行的对象有两种:Inter-query(查询间的并行)、Intra-query(查询内的并行)。并行的层次可以有以下三种:
- 指令并行(super scalar execution):超流水线;CPU执行指令分为4个阶段:Instruction Fetch(IF),Instruction Decode(ID),Execute(EX),WriteBack(WB);每个阶段操作的对象不同,在一个CPU的时钟周期中,就可以对不同指令的不同执行阶段进行同时执行。
- 数据并行(SIMD): 单指令多数据;一个指令同时处理多个数据。
- 线程并行:多线程执行;线程并行有两种方式:Temporal multithreading、Simultaneous multithreading;主要区别就是在一个指令周期里CPU上执行的指令是来自一个线程还是多个线程,前者来自一个线程,后者来自多个线程。
计算相关的存储层的读写开销对整体的lantency有显著的影响,按照距离CPU的远近,有cache size、TLB size、page size和table size。另外page内部的layout,以及table在磁盘中的layout也是会对整体性能有所影响。之前基于磁盘的数据IO是主要的瓶颈,但是对于内存数据库,IO不再是瓶颈了,那么在设计数据库算法的时候,如果能充分适配靠近CPU的cache,优化cache miss,就很有必要了。
本文描述了在多核环境下的Join算法的新的设计思路,针对性的优化cache miss、TLB miss,获得更快的执行速度。
Join 算法概述
假设我们有两张表R,S;分别有M,N个块;以及m,n个元组。常规的Join算法有三种:NestLoop,SortMerge,Hash。基本从名字上我们就能够了解到算法的机制。当进行选择的时候还会根据是否有索引,或者是否已经有序来选择合适的算法。数据库主要的性能瓶颈是IO,这里简单介绍一下各种算法的IO代价:
- Simple NestLoop:R作为外表,从R中取元组和整个S进行match;这样整体的IO代价为
O(M+m*N)。当表比较小时我们可以采取这种算法。 - Blocked NestLoop :从外存中取块和整个S进行Match;这样整体的IO代价为
O(M+M*N)。 - Indexed NestLoop :当某个表上存在索引时,将其作为内表;设查索引的代价为C,这样整体的IO代价为
O(M+m*C)。 - SortMerge:如果两个表都排好序了,那么排序的代价为0;假设两个表都没有拍好序,这里整体的代价就是
O(M+N+sortCost)。 - HashJoin:取决于HashTable能否在内存中放下(是否对HashTable进行分块),以及我们是否提前得知了HashTable的大小(采用静态Hash还是动态Hash)。具体的IO代价是不同的,下节会详细介绍。
简单介绍了算法,每个Join算法都是基于某些列进行匹配,然后定位到Match的Value,关于JoinValue的存储,一般就两种方案。
- Full Tuple : 避免match之后,再次取数据;一个块中存储的元组数比较少,并且不容易压缩。
- Tuple Identifier:对于列存的DBMS,不需要取出查询无关的列;并且当Join选择率低的时候,更加有效。易于压缩。
Hash Join
Hardware-unaware
Simple Hash Join
通常来说,R与S两张表进行HashJoin分为两步:
- Build:对于R,建立一个HashTable
- Probe:遍历S,计算Tuple的Hash值,然后从R的HashTable进行匹配。
这就是传统HashJoin,这和底层硬件没有任何适配。HashTable 查找复杂度是O(1),每个关系表扫描一次,那么整个算法的复杂度为O(|R|+|S|)。
如何处理内存不足的情况?
当内存放不下HashTable时,我们首先先将HashTable进行分块;R和S读取到内存中,按照哈希函数h1将元组放到对应块中,然后写回磁盘;这里会对表进行读和写,所以整体的IO代价为
2*O(M+N)。最后,按个读取HashTable的每个块,然后进行Match;因此整体的HashJoin的代价就是
3*O(M+N)。另外,这里如果某个HashTable的块,在内存中放不下的话,再次按照另一个哈希函数h2进行再次分块(RECURSIVE PARTITIONING)。
Parallel No-Partition Hash Join
在传统HashJoin上,我们可以在Build阶段和Probe加上并行;
- Build:将R分成等长的若干块,然后将这些数据库交给N个线程分别计算Hash,然后写入到线程共享的HashTable中。
- 等待所有线程结束后(thread barrier),然后N个线程同时对S进行Hash计算,然后再共享的HashTable中找匹配。
在这个并行算法中,每个HashTable都是共享么,那么线程之间就需要同步。每个线程想要修改HashTuple,需要获取该Tuple上的Latch。但是由于HashTable可能比较大,并且在Probe阶段都是只读的,其实锁竞争代价还是比较小的。那么对于一个有N核的系统来说,算法复杂度就是O((|R|+|S|)/N),这个算法叫NoPartitioning Join。
Hardware-aware join
Partition HashJoin
上述算法的基本点就是先生成一个较大的HashTable,那么在内存中对HashTable的随机访问就可能造成较多的CacheMiss。因此,为减少CacheMiss,提出了将HashTable切分为若干个CacheSize大小的块,至此原HashJoin就加了Partition的前置步骤,如下图:
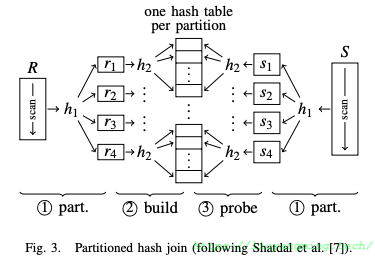
这个算法可称为Partition HashJoin,分为三步。
- Partition:按照哈希函数$h_1$,将R和S分别划分为若干个子块$r_i$和$s_j$(由于基于同一个哈希函数进行分区,这样$r_i$和$s_j$之间不会有交集,这样可以分别处理)。
- Build:对于每个$r_i$,按照哈希函数$h_2$,建立哈希表$h_i$(这里是使用不同的哈希函数)。
- Probe:对于每个$s_j$,按照哈希函数$h_2$,在相应的$h_i$中找匹配。
这个算法在Build阶段生成的哈希表$h_i$可以装进cpu cache中,那么可以有效减少CacheMiss。
但是引入的Partition阶段,可能会将各个Partition放在不同的内存页上;在虚拟内存映射表中对于每一页都需要一个条目,那么,如果有很多partition,就会有很多条目;而虚拟内存映射表也有自己的缓存,叫TLB,条目过多,TLB就会溢出,导致最终的TLB MISS;
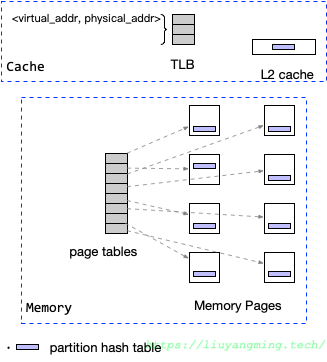
因此,可用的TLB条目大小决定了可以高效使用的分区数的上限,研究学者进一步考虑了Partition阶段的TLB的影响,最终提出了RadixJoin算法。
Radix Join
Radix join通过多次(一般来说两到三次即可)radix-partition,得到不超过TLB容量的partition。如下图。
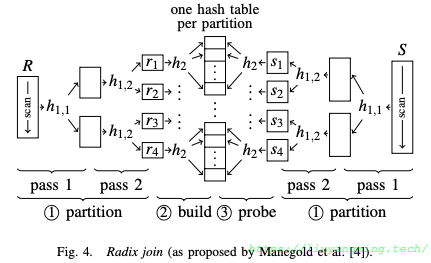
Radix Partition
Radix这里可以理解为JoinKey的某几个bit位,那么,什么是Radix Partition?
举个例子:我们有一个表A,其join key为[07,18,19,07,03,11,15,10]。要对A进行radix partition,执行起来有三步:
- 统计直方图,统计每个Radix取值下的元组数。我们以十位数作为本次的radix,进行统计,这里可以将A进行等分,然后并行统计。
- 汇总统计结果,得到每个radix取值对应的序列号:
r0,r1,r2,…,rn的前缀和序列:S0,S1,S2,...,Sn;统计结果为:count(radix=1)=3,count(radix=0)=5,那么,index(radix=0)=0,index(radix=1)=5。 - 基于统计结果,对原tuple的位置重新调整。进而就将表进行的分区,得到两个分区:[07,07,03,11,15,10,18,19]。
- 回到1,换一个radix,再次进行,直到划分出了特定数目的分区。
基于Radix进行分区后,整个Partition还是在一整块内存区域,避免了零散的内存Page导致的TLB miss。
最后,整个算法还是分为三步:
- Radix Partition:对R和S进行Radix Partition,得到不超过TLB条目的子表;
- Build:对于每个$r_i$,按照哈希函数$h_2$,建立$r_i$的的哈希表$h_i$。
- Probe:对于每个$s_i$,按照哈希函数$h_2$,在相应的hi中找匹配。
相比较于原来的partition hashjoin,radix join其实就是通过提前统计各个partition的大小,将其连续摆放,这样避免了分散的Partition Page导致的TLBMiss,并且其可并行执行。
以上,over;至于具体的性能差异可以直接参考论文。